The Solow growth model was introduced by two very famous economists named Robot Solow and Trevor Swan in the year 1956. The Solow growth model is also known as the Swan growth model. This model is considered to be of great importance in macroeconomics. The Solow growth model is usually used in the long run, and it analyzes the economic growth of the country. The main factors that are focused on in the model include capital growth, labor or the total growth in population and the increase that occurs in the rate of productivity due to technological factors. In simple words, the Solow growth model is a production function.

 

What is Solow Growth Model

The Solow Growth Model is an exogenous neoclassical economic growth model that attempts to explain the growth of a country's economy by looking at capital accumulation, labor or population growth, and increases in productivity largely driven by technological progress. More on wikipedia.

The Solow Growth Model: Assumptions, Solutions and Predictions

Also Read: Fisher’s Theory of Interest Rates [Explained with examples]

The Solow growth model is a neoclassical model in the capital and labor are used at a constant scale to produce the output. The model also assumes that at the beginning the economy has a minimal amount of capital stock and after every specified period this capital tends to increase by using the savings until the economy reaches a steady level. At the steady state, the deprecation becomes equal to the savings. This model is based on the model of Harrod-Domar model. The model starts with a general Cobb-Douglas equation.

In this equation A indicates multifactor productivity, K indicates the contribution of capital, L represents the contribution of labor, and a and b are always less than 1, this proves that there is a diminishing marginal return of these factors. Whereas a + b represents constant returns to scale.

The Solow model states that the increase in output (Q) could be initiated due to the following three reasons:-

• An increase in the force of Labor (L) but would also imply that the output per worker will decrease Q/L. This is due to the factor of diminishing marginal returns.
• An increase in capital accumulation (K), and an increase in the total stock of capital increases both the output and Q/L.
• An increase in A (multifactor productivity) has increased the overall output.

In order to observe the output per worker better, the Solow growth equation can also be written as,

As we know that a + b = 1, we can write this equation as a = 1 – b. Then Substituting 1 – b = a in the equation. We get,

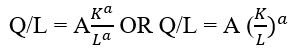
Substituting q as Q/L and K as K/L in the equation we get,

 

Assumptions for the model

Following are the assumptions for the Solow Growth model:-

• The population increases at a constant rate. Hence, we can use N to represent the total population (current and future). For example, if the current population is 1000 and the growth rate is 3%, then the future population would be 1003.
• All the consumers in the economy divide their incomes into two parts. One for consumption and one for savings. Each consumer saves a fixed ratio of their income ‘s’ and spends the rest of the income. Consumption is indicated by C. For example, if a consumer has a total income of $100 and he saves 20% of his income and spends 80%. Than $20 will go into saving and $80 will be spent monthly.
• The technology used for production by all the firms in the economy is the same. Hence the equation Q = AF(K, L).
• The rate of the present stock of capital is denoted by K, the future stock of capital is denoted by K’, the rate at which the capital is depreciating is denoted by d and lastly, the rate of investment is denoted by I. The equation becomes K’ = K(1-d’) + I.

 

Solution of the Solow growth model

a) Considering the production function equation Q = AK^bL^(1-b) and the assumption that all the firms in the economy are competitive, which means that they are all “price-takers”, b indicates the share of income that is utilized for the accumulation of capital.

b) According to the assumption that all firms are competitive, we get the following equation.

• The income-expenditure equation can be written as Y = C + I in equilibrium I = sY.
• Substituting I = sY in the equation of capital accumulation K’ = (1 – d) K + sY. The equation in per worker terms can be written as (1 + g) k’ = (1 – d) k + sy = (1-d) k + saf (k) = (1-d) k+ sa.
• The steady-state value of capital per worker and the steady state level of output produced per worker can be written as

K* = (sa/ g + d) ^1/(1-b)

 

Predictions made by the Solow Growth model

• The rate of countries will increase exponentially in the beginning when they first start to accumulate capital and this growth rate will start to decrease as the accumulation process continues. This is due to the diminishing marginal returns.
• Countries will gain more momentum in their output per capita and their standard of living. For example, countries like Hong Kong and Singapore have increased their rate of output per capita exponentially over the past few years. The lifestyle of people in these countries has improved significantly matching that of the developed countries. When countries reach a steady state of production, they all tend to have almost the exact living standards.

 

Conclusion

Investment, saving, and consumption are very important factors for economic growth. An increase in savings tends to increase investment in the long run and an increase in investment further increases the production or total output within the economy. In the short run investment and savings impact the national income and total output. But according to the Solow growth model which focuses on the long run, investment and savings do not impact the total output. The Solow growth model assumes that full employment exists and that all the labour and capital available in the country are being utilized.

The Solow growth model is considered to be one of the most important models in economics. This theory is especially important for developing countries like India which invest its savings for capital and projects. After a certain time, the country witnessed immense economic growth and due to that, the lifestyles of the population within the country have significantly improved. Even though the Solow Growth model is important for developing nations, it also has some insight for the already developed nations as wealth and capital is also required to maintain a specific level of output.